- Решение задач интерполяции и аппроксимации с использованием кривых Безье
- Интерполяция с помощью кривых Безье
- Преимущества использования сплайнов Безье для интерполяции⁚
- Аппроксимация с помощью кривых Безье
- Выбор степени кривой Безье для аппроксимации⁚
- Сравнение интерполяции и аппроксимации
- Практическое применение
- Облако тегов
Решение задач интерполяции и аппроксимации с использованием кривых Безье
В мире компьютерной графики, CAD-систем и моделирования кривые Безье занимают особое место. Их элегантность и гибкость позволяют создавать плавные и точные кривые, идеально подходящие для решения задач интерполяции и аппроксимации. Эта статья посвящена детальному разбору применения кривых Безье в этих задачах, раскрывая их преимущества и подводные камни. Мы рассмотрим, как с помощью относительно простого математического аппарата можно добиться впечатляющих результатов в построении сложных геометрических форм.
Интерполяция и аппроксимация – два фундаментальных понятия в математическом моделировании. Интерполяция предполагает построение кривой, проходящей точно через заданные точки. Аппроксимация, в свою очередь, стремится к созданию кривой, которая наилучшим образом приближает заданный набор точек, не обязательно проходя через них все.
Интерполяция с помощью кривых Безье
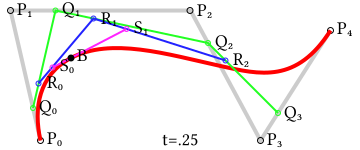
Для интерполяции с использованием кривых Безье часто применяются сплайны Безье. Это набор кривых Безье, соединенных таким образом, чтобы обеспечить плавный переход между ними. Каждая кривая Безье определяется набором контрольных точек. Изменение положения этих точек позволяет легко корректировать форму кривой. Однако, простая цепочка кривых Безье не всегда гарантирует плавность соединения, поэтому используются различные методы обеспечения непрерывности первого и второго порядков (C1 и C2 непрерывность).
Одним из распространенных методов является использование кубических сплайнов Безье. Кубическая кривая Безье определяется четырьмя контрольными точками. Для интерполяции n точек потребуется n-1 кубическая кривая Безье. Выбор контрольных точек, обеспечивающий плавный переход, является ключевым моментом в этом процессе. Существуют различные алгоритмы, позволяющие вычислить оптимальное расположение контрольных точек, обеспечивая требуемую гладкость кривой.
Преимущества использования сплайнов Безье для интерполяции⁚
- Простота реализации и вычислений.
- Гибкость в управлении формой кривой.
- Возможность обеспечения высокой степени гладкости.
- Широкая распространенность и поддержка во многих программных библиотеках.
Аппроксимация с помощью кривых Безье
В задачах аппроксимации кривая Безье не обязана проходить через все заданные точки. Цель – найти кривую, которая наилучшим образом приближает данные точки, минимизируя некоторую меру отклонения. Здесь также могут использоваться сплайны Безье, но подход к выбору контрольных точек будет отличаться от интерполяции.
Один из распространенных методов аппроксимации – метод наименьших квадратов. В этом методе мы стремимся минимизировать сумму квадратов расстояний от заданных точек до аппроксимирующей кривой Безье. Это приводит к системе нелинейных уравнений, решение которых может потребовать итеративных методов, таких как метод Ньютона-Рафсона.
Выбор степени кривой Безье для аппроксимации⁚
Степень кривой Безье влияет на ее гибкость и точность аппроксимации. Более высокая степень позволяет приблизить более сложные формы, но может привести к увеличению вычислительной сложности и появлению нежелательных осцилляций. Выбор оптимальной степени – это компромисс между точностью и вычислительной эффективностью.
Сравнение интерполяции и аппроксимации
| Характеристика | Интерполяция | Аппроксимация |
|---|---|---|
| Прохождение через точки | Кривая проходит через все точки | Кривая не обязательно проходит через все точки |
| Цель | Точное воспроизведение данных | Наилучшее приближение данных |
| Чувствительность к шуму | Высокая, шум может сильно исказить кривую | Низкая, кривая сглаживает шум |
Выбор между интерполяцией и аппроксимацией зависит от конкретной задачи. Если необходима высокая точность и воспроизведение всех данных, то следует использовать интерполяцию. Если же данные содержат шум или требуется сглаживание, то предпочтительнее аппроксимация.
Практическое применение
Кривые Безье широко применяются в различных областях⁚ компьютерной графике (рисование, анимация), CAD-системах (проектирование), робототехнике (траектории движения), обработке изображений и многих других. Их универсальность и простота реализации делают их незаменимым инструментом для решения широкого круга задач.
Кривые Безье представляют собой мощный инструмент для решения задач интерполяции и аппроксимации. Понимание их свойств и методов применения позволяет создавать плавные, точные и эффективные модели сложных геометрических форм. Выбор между интерполяцией и аппроксимацией зависит от специфики задачи и требований к точности. Дальнейшее изучение различных алгоритмов и методов оптимизации позволит вам эффективно использовать кривые Безье в ваших проектах.
Рекомендуем вам ознакомиться с другими нашими статьями, посвященными алгоритмам построения кривых Безье, методам оптимизации и примерам практического применения в различных областях.
Облако тегов
| Кривые Безье | Интерполяция | Аппроксимация |
| Сплайны | Компьютерная графика | CAD |
| Моделирование | Алгоритмы | Математика |